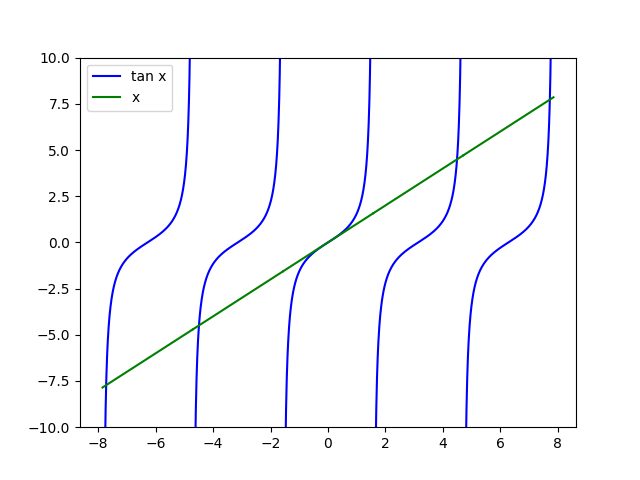
I read something recently that said in passing that the solutions to the equation tan x = x are the zeros of the Bessel function J3/2. That brought two questions to mind. First, where have I seen the equation tan x = x before? And second, why should its solutions be the roots of a Bessel function.
The answer to the first question is that I wrote about the local maxima of the sinc function three years ago. That post shows that the derivative of the sinc function sin(x)/x is zero if and only if x is a fixed point of the tangent function.
As for why that should be connected to zeros a Bessel function, that one’s pretty easy. In general, Bessel functions cannot be expressed in terms of elementary functions. But the Bessel functions whose order is an integer plus ½ can.
For integer n,
So when n = 1, we’ve got the derivative of sinc right there in the definition.