Recamán’s sequence

I recently ran into Recamán’s sequence. N. J. A. Sloane, the founder of the Online Encyclopedia of Integer Sequences calls Recamán’s sequence one of his favorites. It’s sequence A005132 in the OEIS.

This sequence starts at 0 and the nth number in the sequence is the result of moving forward or backward n steps from the previous number. You are allowed to move backward if the result is positive and a number you haven’t already visited. Otherwise you move forward.

Here’s Python code to generate the first N elements of the sequence.

    def recaman(N):
        a = [0]*N
        for n in range(1, N):
            proposal = a[n-1] - n
            if proposal > 0 and proposal not in set(a):
                a[n] = proposal
            else:
                a[n] = a[n-1] + n
        return a

For example, recaman(10) returns

    [0, 1, 3, 6, 2, 7, 13, 20, 12, 21]

There’s a Numberphile video that does two interesting things with the sequence: it visualizes the sequence and plays a representation of the sequence as music.

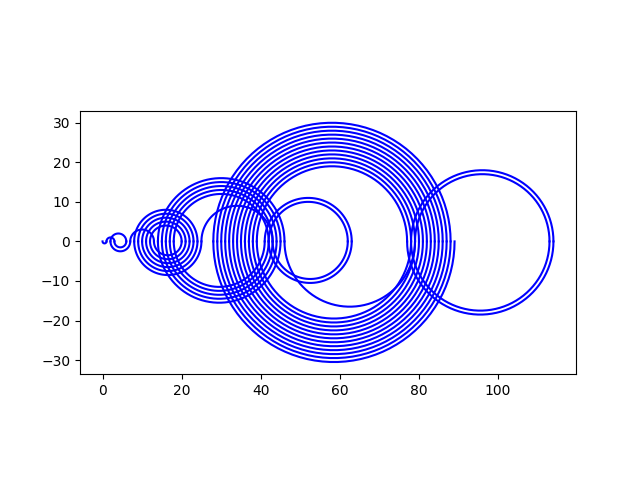
The rules for the visualization are that you connect consecutive elements of the sequence with circular arcs, alternating arcs above and below the numberline.

Here’s code to reproduce an image from the video.

    import numpy as np
    import matplotlib.pyplot as plt
    
    def draw_arc(a, b, n):
        c = (a + b)/2
        r = max(a, b) - c
        t = np.linspace(0, np.pi) * (-1)**(n+1)
        plt.plot(c + r*np.cos(t), r*np.sin(t), 'b')
           
    N = 62
    a = recaman(N)
    for n in range(N-1):
        draw_arc(a[n], a[n+1], n)
    plt.gca().set_aspect("equal")
    plt.show()

Here’s the output:

To create a music sequence, associate the number n with the nth note of the chromatic scale. You can listen to the music in the video; here’s sheet music made with Lilypond.

Update

Here is another Recamán visualization going further out in the sequence. I made a few aesthetic changes at the same time.

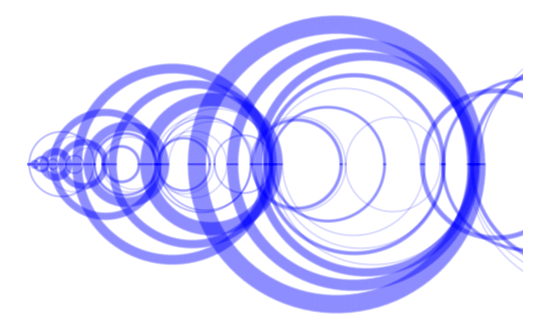
I’ve also made higher resolution versions of the images in this post. Here are SVG and PDF versions of the first visualization.

Here is a PDF of the sheet music.

And here are SVG and PDF versions of the new visualization.