Five years ago I wrote a blog post entitled Logisitic bifurcation diagram in detail. Looking back at that post it doesn’t seem to be that much “in detail,” though it does go into more detail than most popular accounts.
The logistic map is given by
f(x) = r x(1 − x)
where x is a variable between 0 and 1 and r is a parameter between 0 and 4.
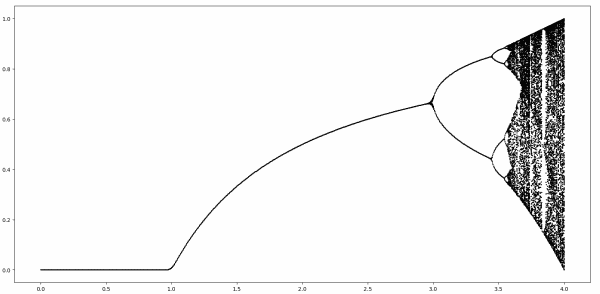
If you look at what happens to values of x as you repeatedly apply the logistic map, computing f(x), f(f(x)), f(f(f(x))), …, things get interesting:
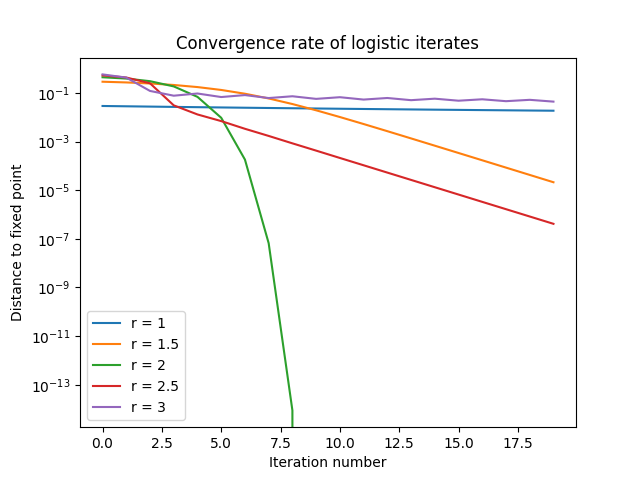
This plot shows where the iterations end up as the parameter r varies. When r ≤ 3 the iterates converge to a single fixed point, assuming you start strictly between 0 and 1. When r is a little bigger than 3 the iterates cycle between two atractor points, then for larger r they bounce between 4 points, then 8, then eventually chaos breaks out. Literally.
In the diagram above, it seems the region where 0 ≤ r ≤ 3 is the simple part. And it is, but it’s not that simple. This post will look a little deeper into what’s happening in this part of the diagram.
Four questions
There is a series of questions we can ask about the convergence of a sequence.
- Does the sequence converge?
- What does it converge to?
- How does it converge qualitatively?
- How rapidly does it converge?
We know that for 0 ≤ r ≤ 3 the iterates converge to a single point. So the answer to the first question is yes.
For 0 ≤ r ≤ 1 the iterates converge to 0. For 0 ≤ r ≤ 3 the iterates converge to (r − 1)/r. This answers the second question.
The third and fourth questions are more interesting.
Qualitative convergence
When 0 ≤ r < 1 the iterates decrease monotonically to 0.
When 1 ≤ r ≤ 2 the convergence is monotone. If x starts out below the fixed point (r − 1)/r then the convergence is monotone increasing. If x starts out above, the sequence is monotone decreasing.
When 2 < r ≤ 3 the convergence is not monotone; the iterates alternately overshoot and undershoot the fixed point once they get sufficiently close. This is because the derivative of f at the fixed point is negative.
Here is a cobweb plot showing that the convergence when r = 2.9 is not monotone.
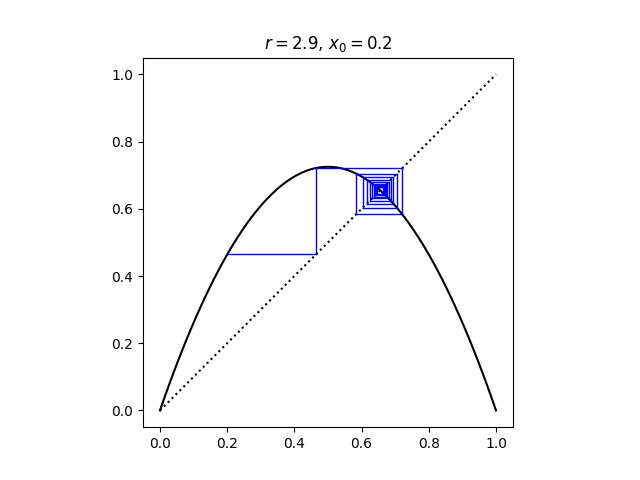
In a cobweb plot, monotone convergence looks like a staircase, and oscillating convergence looks like a spiral.
Speed of convergence
In the region 0 < r < 1, convergence is like rn.
In the region 1 < r < 2, convergence is like (2 − r)n.
In the region 2 < r < 3, convergence is also like (2 − r)n, which now alternates sign.
The exceptional cases are r = 1, 2, and 3. Convergence is very slow for r = 1 and 3, and very fast for r = 2.
When r = 2, the distance to the fixed point squares at each step, so convergence is quadratic.