Logarithm approximation curiosity

I’ve written before about three simple approximations for logarithms, for base 10

log₁₀(x) ≈ (x – 1)/(x + 1)

base e,

log_e(x) ≈ 2(x – 1)/(x + 1)

and base 2

log₂(x) ≈ 3(x – 1)/(x + 1).

These can be used to mentally approximate logarithms to moderate accuracy, accurate enough for quick estimates.

Here’s what’s curious about the approximations: the proportionality constants are apparently wrong, and yet the approximations are each fairly accurate.

It is not the case that

log_e(x) = 2 log₁₀(x).

In fact,

log_e(x) = log_e(10) log₁₀(x) = 2.3 log₁₀(x)

and so it seems that the approximation for natural logarithms should be off by 15%. But it’s not. The error is less than 2.5%.

Similarly,

log₂(x) = log₂(10) log₁₀(x) = 3.32 log₁₀(x)

and so the approximation for logarithms base 2 should be off by about 10%. But it’s not. The error here is also less than 2.5%.

What’s going on?

First of all, the approximation errors are nonlinear functions of x and the three approximation errors are not proportional. Second, the approximation for log_b(x) is only good for 1/√b ≤ x ≤ √b. You can always reduce the problem of calculating log_b(x) to the problem of calculating the log in the range 1/√b ≤ x ≤ √b and so this isn’t a problem.

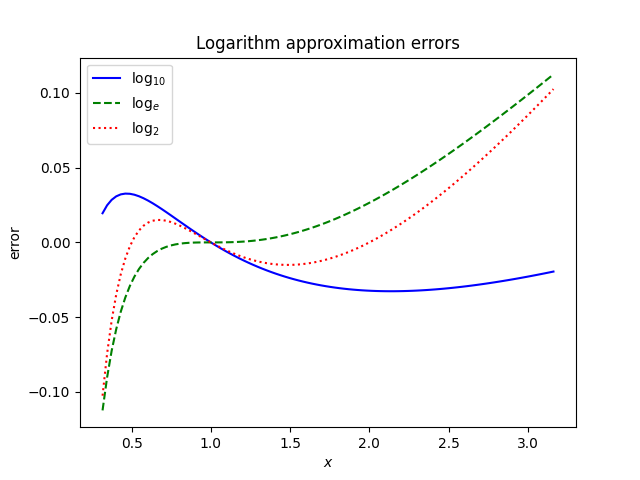
Here’s a plot of the three error functions.

This plot makes it appear that the approximation error is much worse for natural logs and logs base 2 than for logs base 10. And it would be if we ignored the range of each approximation. Here’s another plot of the approximation errors, plotting each over only its valid range.

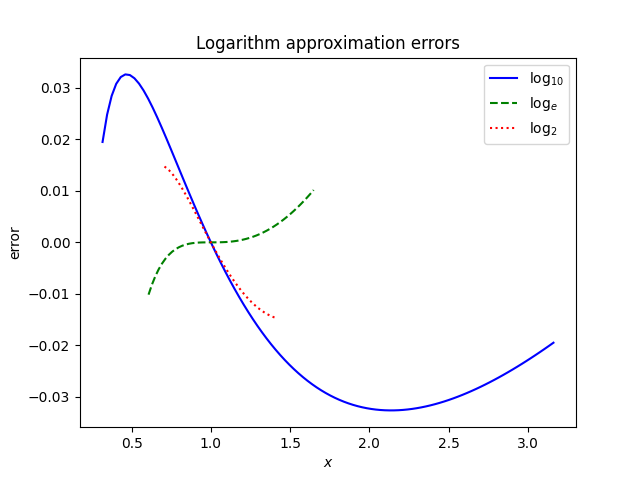
When restricted to their valid ranges, the approximations for logarithms base e and base 2 are more accurate than the approximation for logarithms base 10. Both errors are small, but in opposite directions.

Here’s a look at the relative approximation errors.

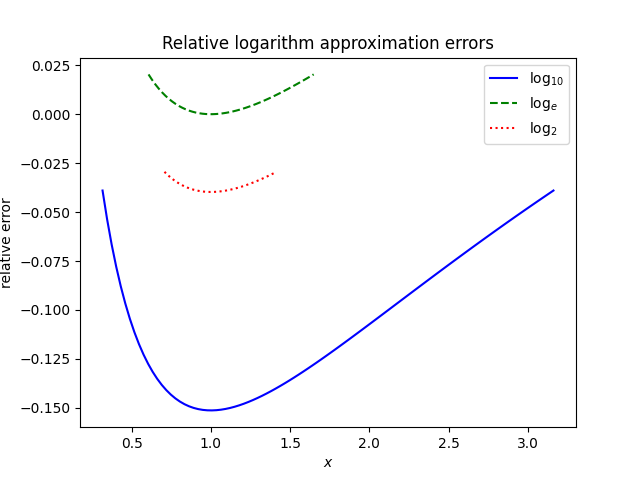
We can see that the relative errors for the log 2 and log e errors are less than 2.5%, while the relative error for log 10 can be up to 15%.