An Archimedian spiral has the polar equation
r = b θ1/n
This post will look at the case n = 1. I may look at more general values of n in a future post. The case n = 1 is the simplest case, and it’s the case I needed for the client project that motivated this post.
In this case the spacing between points where the spiral crosses an axis is constant. Call this constant h. Then
h = 2πb.
For example, when rolling up a carpet, h corresponds to the thickness of the carpet.
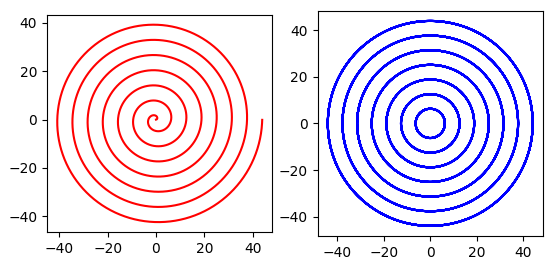
Suppose θ runs from 0 to 2πm, wrapping around the origin m times. We could approximate the spiral by m concentric circles of radius h, 2h, 3h, …, mh. To visualize this, we’re approximating the length of the red spiral on the left with that of the blue circles on the right.
We could approximate this further by saying we have m/2 circles whose average radius is πmb. This suggests the length of the spiral should be approximately
2π²m²b
How good is this approximation? What happens to the relative error as θ increases? Intuitively, each wrap around the origin is more like a circle as θ increases, so we’d expect the approximation to improve for large θ.
According to Mathworld, the exact length of the spiral is
πbm √(1 + (2πm)²) + b arcsinh(2πm) /2
When m is so large that we can ignore the 1 in √(1 + (2πm)²) then the first term is the same as the circle approximation, and all that’s left is the arcsinh term, which is on the order of log m because
arcsinh(x) = log(x + (1 + x²)1/2).
So for large m, the arc length is on the order of m² while the error is on the order of log m. This means the relative error is O( log(m) / m² ). [1]
We’ve assumed m was an integer because that makes it easier to visual approximating the spiral by circles, but that assumption is not necessary. We could restate the problem in terms of the final value of θ. Say θ runs from 0 to T. Then we could solve
T = 2πm
for m and say that the approximate arc length is
½ bT²
and the exact length is
½ bT(1 + T²)1/2 + ½ b arcsinh(T).
The relative approximation error is O( log(T) / T² ).
Related posts
[1] The error in approximating √(1 + (2πm)²) with 2πm is on the order of 1/(4πm) and so is smaller than the logarithmic term.