If any field of mathematics has been thoroughly combed over, it’s Euclidean geometry. But once in a while someone will come up with a new theorem that seems it should have been discovered centuries ago.
Here’s a theorem conjectured by Paul Erdős in 1935 and proved by Louis Mordell later the same year.
If from a point O inside a given triangle ABC perpendiculars OD, OE, OF are drawn to its sides, then
OA + OB + OC ≥ 2(OD + OE + OF).
Equality holds if and only if triangle ABC is equilateral.
To put it more succinctly,
From any interior point, the distances to the vertices are at least twice the distances to the sides.
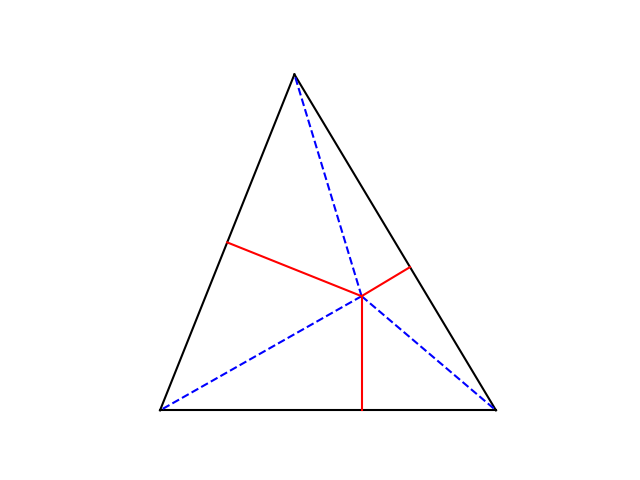
Here’s an illustration. In the figure above, the theorem says the dashed blue lines together are more than twice as long as the solid red lines.
In the units I used in drawing the figure above, the blue lines have combined length 9.5 and the red lines have combined length 4.7.
Hojoo Lee gave an elementary proof of the Erdős-Mordell theorem in 2001 that takes about one printed page [1].
In my opinion the Erdős-Mordell theorem feels like a theorem an ancient geometer could have discovered and proved. Here’s a generalization of the theorem that feels much more contemporary [2].
Let Ri be the distance from an interior point O to the ith vertex and ri the distance to the side opposite the ith vertex. Let λ1, λ2, and λ3 be any three positive real numbers. Then
When all the λs equal 1, we get the original Erdős-Mordell theorem.
You could say the weighted distances to the vertices are at least twice the weighted distances to the sides, but you have to say more about the weights, and in general the weights work differently on both sides of the inequality.
[1] Hojoo Lee. Another Proof of the Erdős-Mordell Theorem. Forum Geometricorum, Volume 1 (2001) p. 7–8
[2] Seannie Dar, Shay Gueron. A Weighted Erdős-Mordell Inequality. The American Mathematical Monthly. Vol. 108, No. 2, Feb., 2001