Distribution of run times for Euclidean algorithm

The worst case run time for the Euclidean algorithm occurs when you give the algorithm a pair of consecutive Fibonacci numbers. The algorithm takes n steps to compute the greatest common divisor of F_n+1 and F_n+2.

The nth Fibonacci number is the nearest integer to φⁿ/√5 where φ = (1 + √5)/2 is the golden ratio. You can take logs and solve for the largest n such that F_n is less than x, subtract 2, and have an upper bound on the number of steps necessary to find the gcd of two numbers less than x.

But what about the average run time, or the distribution of run times?

For large x, the distribution of number of steps needed to calculate the gcd of two numbers 0 < a < b < x using the Euclidean algorithm is approximately normal with mean

12 log(2) log(b) / π².

See, for example, [1].

Let’s illustrate this with a simulation. Here’s Python code to return the number of steps used in computing gcd(a, b).

    def euclid(a, b):
        steps = 0
        while a != 0:
            a, b = b%a, a
            steps += 1
        return steps # gcd = b

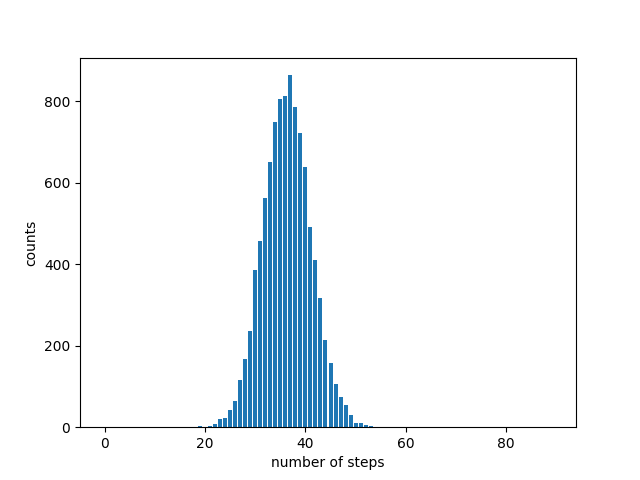
I generated 10,000 pairs of random integers less than 2⁶³ (because the maximum signed 64 bit integer is 2⁶³ − 1) and plotted a histogram of the run times.

I got a nice bell curve with mean 36.3736. The theoretical mean is 0.8428 log(2⁶³) = 36.8021.

[1] Doug Hensley. The Number of Steps in the Euclidean Algorithm. Journal of Number Theory 49. 142–182 (1994).