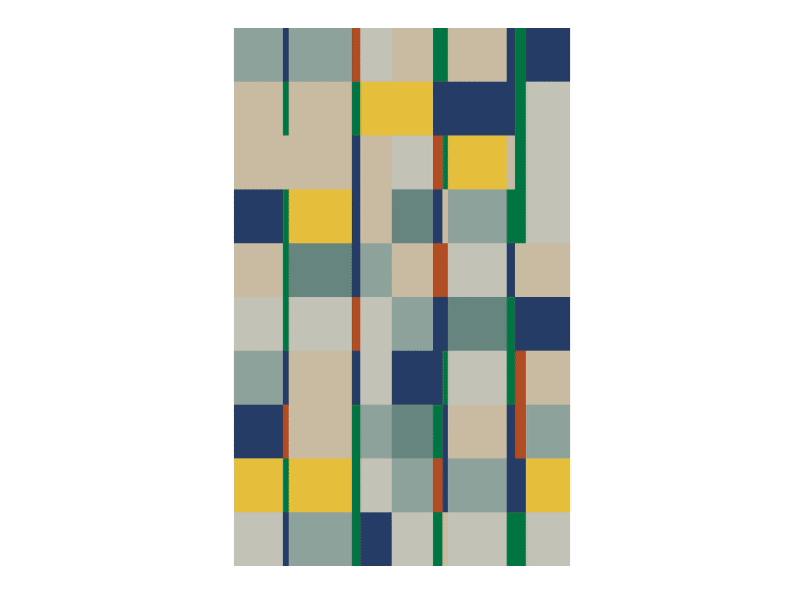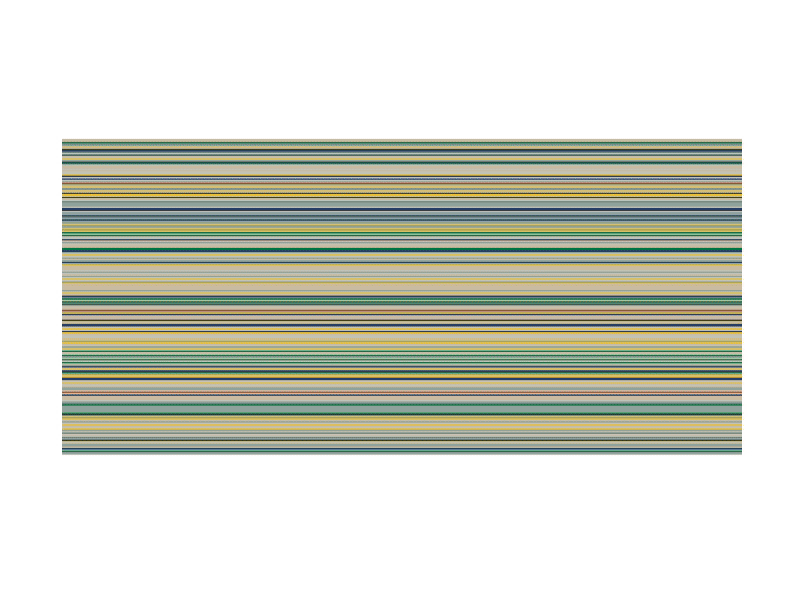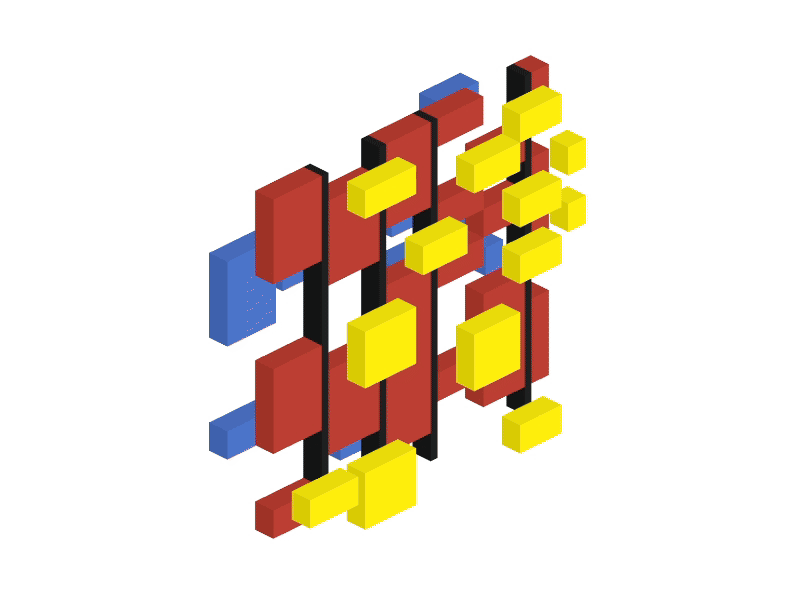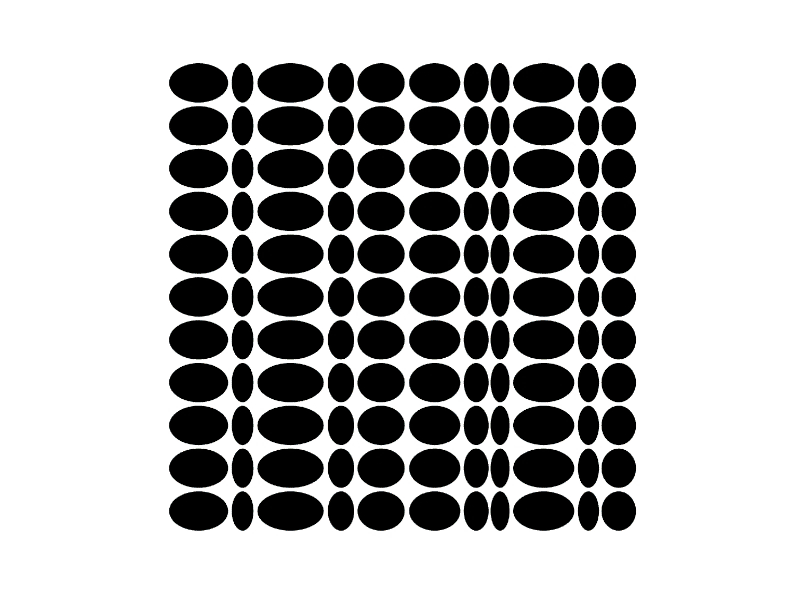In this tutorial, we will create a generative artwork inspired by the incredible Brazilian artist Lygia Clarke. Some of her paintings, based on minimalism and geometric figures, are perfect to be reinterpreted using a grid and generative system:

The possibilities of a grid system
It is well known, that grids are an indispensable element of design; from designing typefaces to interior design. But grids, are also essential elements in other fields like architecture, math, science, technology, and painting, to name a few. All grids share that more repetition means more possibilities, adding detail and rhythm to our system. If for example, we have an image that is 2×2 pixels we could have a maximum of 4 color values to build an image, but if we increase that number to 1080×1080 we can play with 1,166,400 pixels of color values.
Examples: Romain Du Roi, Transfer Grid, Cartesian Coordinate System, Pixels, Quadtree, Mesh of Geometry.
Project Setup
Before starting to code, we can set up the project and create the folder structure. I will be using a setup with vite, react, and react three fiber because of its ease of use and rapid iteration, but you are more than welcome to use any tool you like.
npm create vite@latest generative-art-with-three -- --template reactOnce we create our project with Vite we will need to install Three.js and React Three Fiber and its types.
cd generative-art-with-three
npm i three @react-three/fiber
npm i -D @types/threeNow, we can clean up the project by deleting unnecessary files like the vite.svg in the public folder, the App.css, and the assets folder. From here, we can create a folder called components in the src folder where we will make our artwork, I will name it Lygia.jsx in her honor, but you can use the name of your choice.
├─ public
├─ src
│ ├─ components
│ │ └─ Lygia.jsx
│ ├─ App.jsx
│ ├─ index.css
│ └─ main.jsx
├─ .gitignore
├─ eslint.config.js
├─ index.html
├─ package-lock.json
├─ package.json
├─ README.md
└─ vite.config.jsLet’s continue with the Three.js / React Three Fiber setup.
React Three Fiber Setup
Fortunately, React Three Fiber handles the setup of the WebGLRenderer and other essentials such as the scene, camera, canvas resizing, and animation loop. These are all encapsulated in a component called Canvas. The components we add inside this Canvas should be part of the Three.js API. However, instead of instantiating classes and adding them to the scene manually, we can use them as React components (remember to use camelCase):
// Vanilla Three.js
const scene = new Scene()
const mesh = new Mesh(new PlaneGeometry(), new MeshBasicMaterial())
scene.add(mesh)// React Three Fiber
import { Canvas } from "@react-three/fiber";
function App() {
return (
<Canvas>
<mesh>
<planeGeometry />
<meshBasicMaterial />
</mesh>
</Canvas>
);
}
export default App;Finally, let’s add some styling to our index.css to make the app fill the entire window:
html,
body,
#root {
height: 100%;
margin: 0;
}Now, if you run the app from the terminal with npm run dev you should see the following:
Congratulations! You have created the most boring app ever! Joking aside, let’s move on to our grid.
Creating Our Grid
After importing Lygia’s original artwork into Figma and creating a Layout grid, trial and error revealed that most elements fit into a 50×86 grid (without gutters). While there are more precise methods to calculate a modular grid, this approach suffices for our purposes. Let’s translate this grid structure into code within our Lygia.jsx file:
import { useMemo, useRef } from "react";
import { Object3D } from "three";
import { useFrame } from "@react-three/fiber";
const dummy = new Object3D();
const LygiaGrid = ({ width = 50, height = 86 }) => {
const mesh = useRef();
const squares = useMemo(() => {
const temp = [];
for (let i = 0; i < width; i++) {
for (let j = 0; j < height; j++) {
temp.push({
x: i - width / 2,
y: j - height / 2,
});
}
}
return temp;
}, [width, height]);
useFrame(() => {
for (let i = 0; i < squares.length; i++) {
const { x, y } = squares[i];
dummy.position.set(x, y, 0);
dummy.updateMatrix();
mesh.current.setMatrixAt(i, dummy.matrix);
}
mesh.current.instanceMatrix.needsUpdate = true;
});
return (
<instancedMesh ref={mesh} args={[null, null, width * height]}>
<planeGeometry />
<meshBasicMaterial wireframe color="black" />
</instancedMesh>
);
};
export { LygiaGrid };A lot of new things suddenly, but do not worry I am going to explain what everything does; let’s go over each element:
- Create a variable called
dummyand assign it to anObject3Dfrom Three.js. This will allow us to store positions and any other transformations. We will use it to pass all these transformations to the mesh. It does not have any other function, hence the namedummy(more on that later). - We add the width and height of the grid as props of our Component.
- We will use a React
useRefhook to be able to reference theinstancedMesh(more on that later). - To be able to set the positions of all our instances, we calculate them beforehand in a function. We are using a
useMemohook from React because as our complexity increases, we will be able to store the calculations between re-renders (it will only update in case the dependency array values update [width, height]). Inside the memo, we have two for loops to loop through the width and the height and we set the positions using theito set up thexposition and thejto set ouryposition. We will minus thewidthand theheightdivided by two so our grid of elements is centered. - We have two options to set the positions, a
useEffecthook from React, or a useFrame hook from React Three Fiber. We chose the latter because it is a render loop. This will allow us to animate the referenced elements. - Inside the
useFramehook, we loop through all instances usingsquares.length. Here we deconstruct our previousxandyfor each element. We pass it to ourdummyand then we useupdateMatrix()to apply the changes. - Lastly, we return an
<instancedMesh/>that wraps our<planeGeometry/>which will be our 1×1 squares and a<meshBasicMaterial/>—otherwise, we wouldn’t see anything. We also set thewireframeprop so we can see that is a grid of 50×86 squares and not a big rectangle.
Now we can import our component into our main app and use it inside the <Canvas/> component. To view our entire grid, we’ll need to adjust the camera’s z position to 65.
import { Canvas } from "@react-three/fiber";
import { Lygia } from "./components/Lygia";
function App() {
return (
<Canvas camera={{ position: [0, 0, 65] }}>
<Lygia />
</Canvas>
);
}
export default App;Our result:
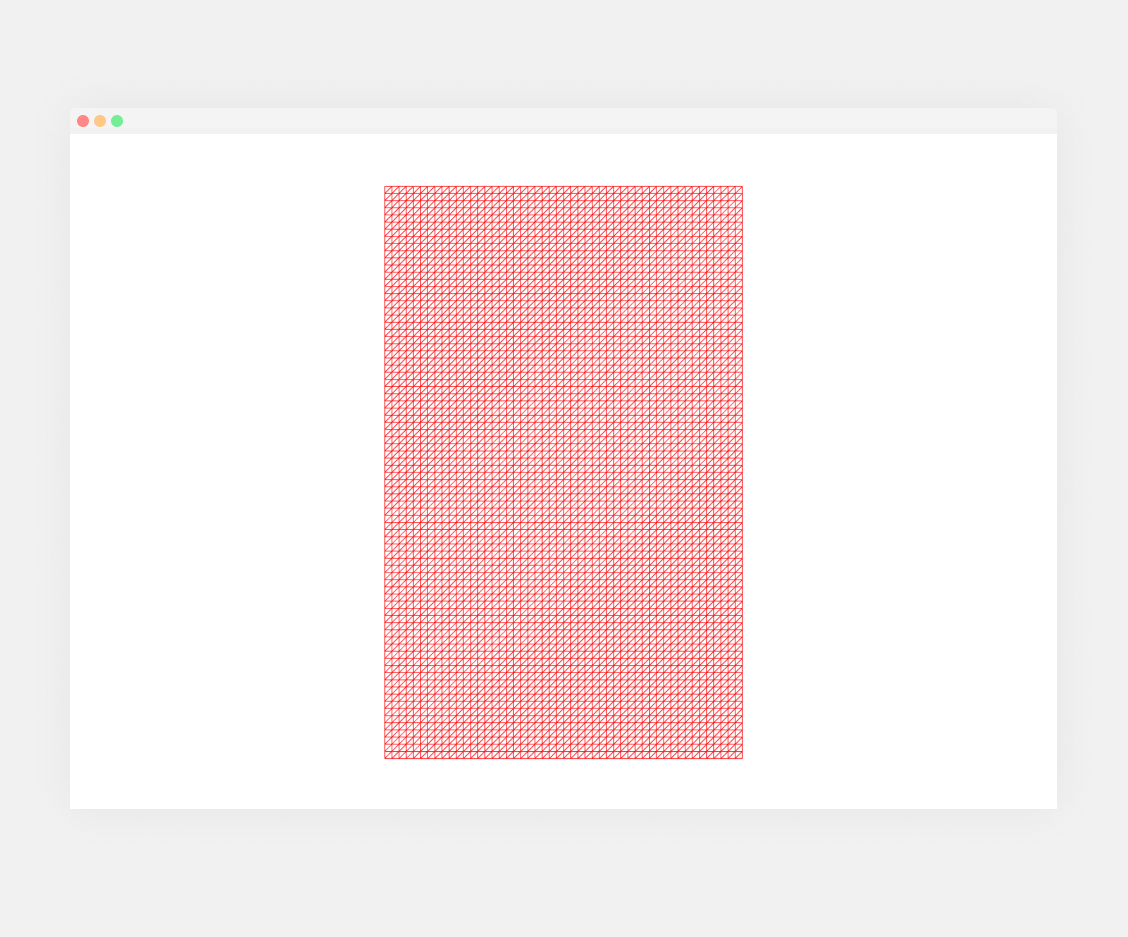
Breaking The Grid
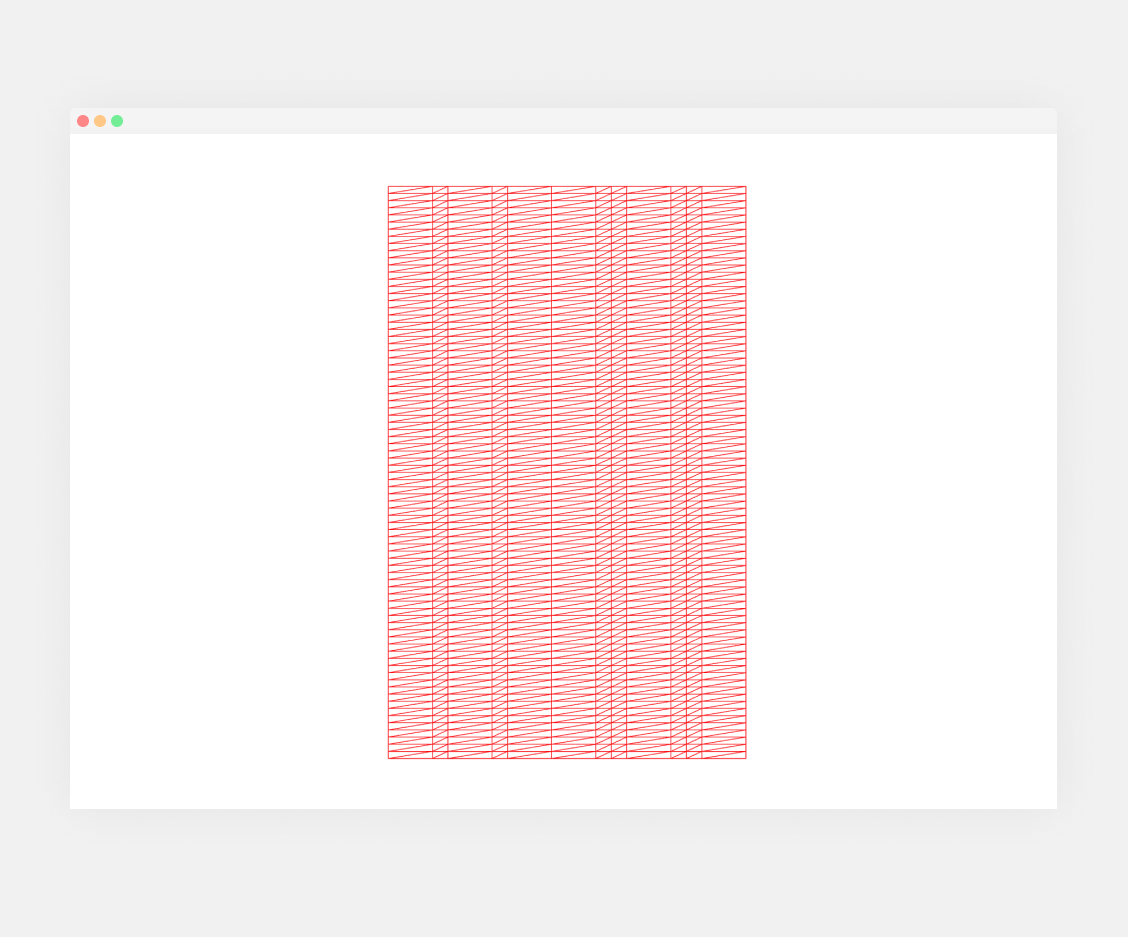
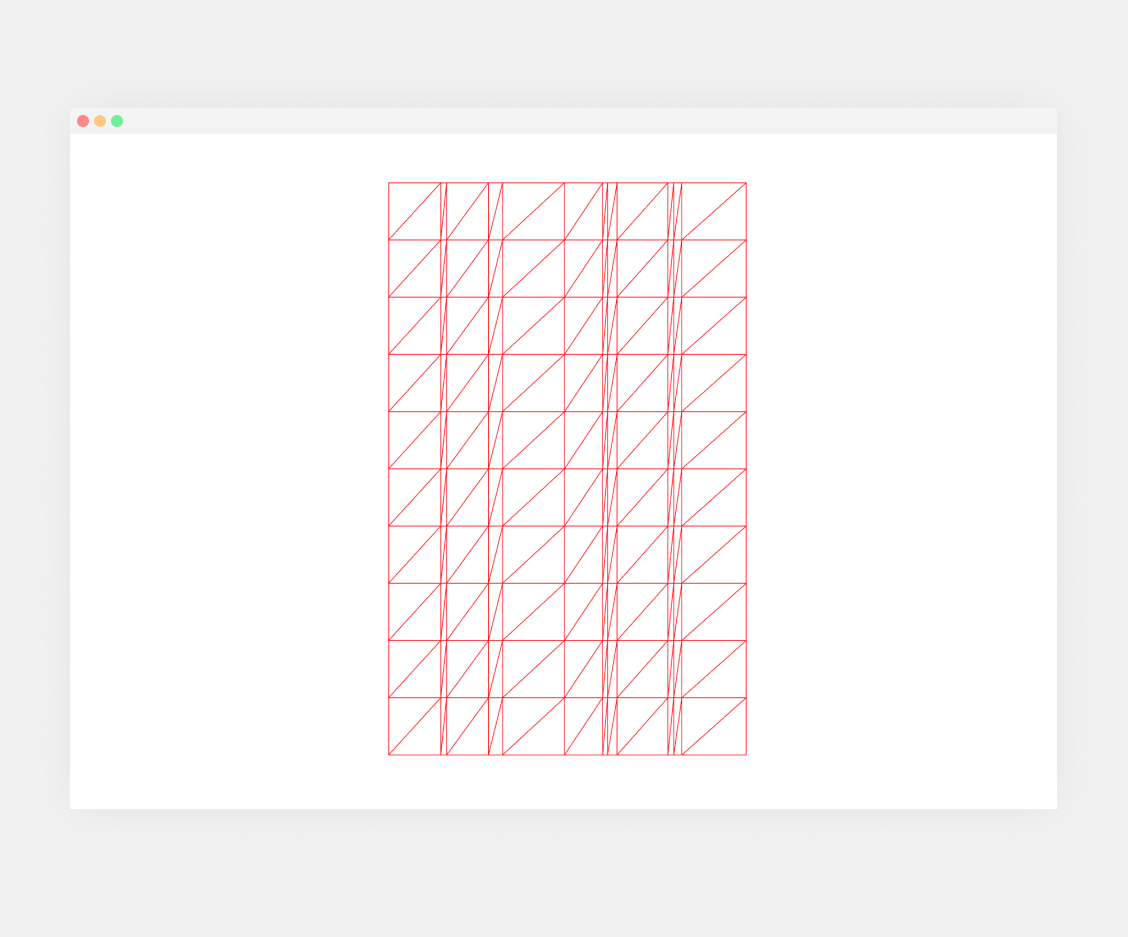
One of the hardest parts in art, but also in any other subject like math or programming is to unlearn what we learned, or in other words, break the rules that we are used to. If we observe Lygia’s artwork, we clearly see that some elements don’t perfectly align with the grid, she deliberately broke the rules.
If we focus on the columns for now, we see that there are a total of 12 columns, and the numbers 2, 4, 7, 8, 10, and 11 are smaller meaning numbers 1, 3, 5, 6, 9, and 12 have bigger values. At the same time, we see that those columns have different widths, so column 2 is bigger than column 10, despite that they are in the same group; small columns. To achieve this we can create an array containing the small numbers: [2, 4, 7, 8, 10, 11]. But of course, we have a problem here, we have 50 columns, so there is no way we can know it. The easiest way to solve this problem is to loop through our number of columns (12), and instead of our width we will use a scale value to set the size of the columns, meaning each grid will be 4.1666 squares (50/12):
const dummy = new Object3D();
const LygiaGrid = ({ width = 50, height = 80, columns = 12 }) => {
const mesh = useRef();
const smallColumns = [2, 4, 7, 8, 10, 11];
const squares = useMemo(() => {
const temp = [];
let x = 0;
for (let i = 0; i < columns; i++) {
const ratio = width / columns;
const column = smallColumns.includes(i + 1) ? ratio - 2 : ratio + 2;
for (let j = 0; j < height; j++) {
temp.push({
x: x + column / 2 - width / 2,
y: j - height / 2,
scaleX: column,
});
}
x += column;
}
return temp;
}, [width, height]);
useFrame(() => {
for (let i = 0; i < squares.length; i++) {
const { x, y, scaleX } = squares[i];
dummy.position.set(x, y, 0);
dummy.scale.set(scaleX, 1, 1);
dummy.updateMatrix();
mesh.current.setMatrixAt(i, dummy.matrix);
}
mesh.current.instanceMatrix.needsUpdate = true;
});
return (
<instancedMesh ref={mesh} args={[null, null, columns * height]}>
<planeGeometry />
<meshBasicMaterial color="red" wireframe />
</instancedMesh>
);
};
export { LygiaGrid };So, we are looping our columns, we are setting our ratio to be the grid width divided by our columns. Then we set the column to be equal to our ratio minus 2 in case it is in the list of our small columns, or ratio plus 2 in case it isn’t. Then, we do the same as we were doing before, but our x is a bit different. Because our columns are random numbers we need to sum the current column width to x at the end of our first loop:
We are almost there, but not quite yet, we need to ‘really’ break it. There are a lot of ways to do this but the one that will give us more natural results will be using noise. I recommend using the library Open Simplex Noise, an open-source version of Simplex Noise, but you are more than welcome to use any other options.
npm i open-simplex-noiseIf we now use the noise in our for loop, it should look something like this:
import { makeNoise2D } from "open-simplex-noise";
const noise = makeNoise2D(Date.now());
const LygiaGrid = ({ width = 50, height = 86, columns = 12 }) => {
const mesh = useRef();
const smallColumns = [2, 4, 7, 8, 10, 11];
const squares = useMemo(() => {
const temp = [];
let x = 0;
for (let i = 0; i < columns; i++) {
const n = noise(i, 0) * 5;
const remainingWidth = width - x;
const ratio = remainingWidth / (columns - i);
const column = smallColumns.includes(i + 1)
? ratio / MathUtils.mapLinear(n, -1, 1, 3, 4)
: ratio * MathUtils.mapLinear(n, -1, 1, 1.5, 2);
const adjustedColumn = i === columns - 1 ? remainingWidth : column;
for (let j = 0; j < height; j++) {
temp.push({
x: x + adjustedColumn / 2 - width / 2,
y: j - height / 2,
scaleX: adjustedColumn,
});
}
x += column;
}
return temp;
}, [width, height]);
// Rest of code...First, we import the makeNoise2D function from open-simplex-noise, then we create a noise variable which equals the previously imported makeNoise2D with an argument Date.now(), remember this is the seed. Now, we can jump to our for loop.
- We add a constant variable called
nwhich equals to ournoisefunction. We pass as an argument the increment (i) from our loop and multiply it by5which will give us more values between -1 and 1. - Because we will be using random numbers, we need to keep track of our remaining width, which will be our
remaningWidthdivided by the number ofcolumnsminus the current number of columnsi. - Next, we have the same logic as before to check if the column is in our
smallColumnslist but with a small change; we use thennoise. In this case, I am using amapLinearfunction from Three.jsMathUtilsand I am mapping the value from[-1, 1]to[3, 4]in case the column is in our small columns or to[1.5, 2]in case it is not. Notice I am dividing it or multiplying it instead. Try your values. Remember, we are breaking what we did. - Finally, if it is the last column, we use our
remaningWidth.
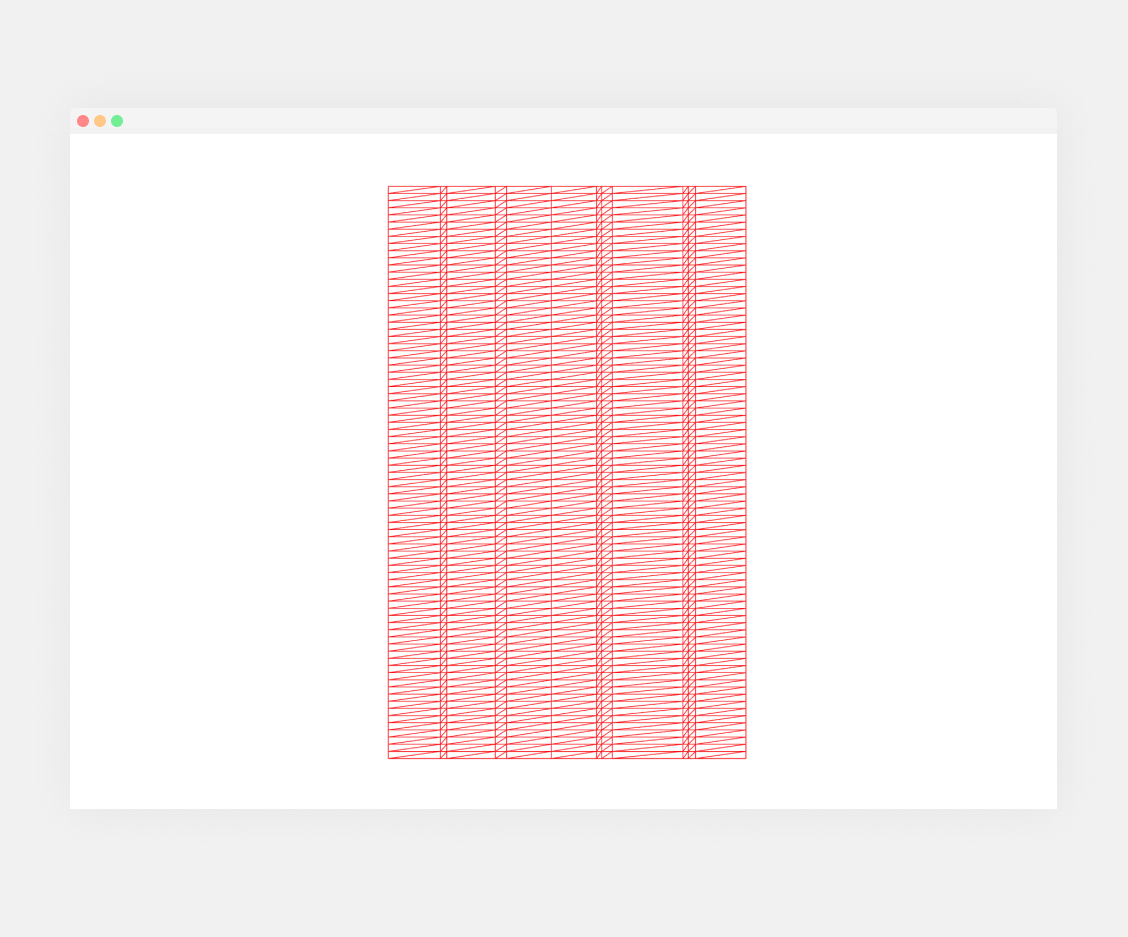
Now, there is only one step left, we need to set our row height. To do so, we just need to add a rows prop as we did for columns and loop through it and at the top of the useMemo, we can divide our height by the number of rows. Remember to finally push it to the temp as scaleY and use it in the useFrame.
const LygiaGrid = ({ width = 50, height = 86, columns = 12, rows = 10 }) => {
...
const squares = useMemo(() => {
const temp = [];
let x = 0;
const row = height / rows;
for (let i = 0; i < columns; i++) {
const n = noise(i, 0) * 5;
const remainingWidth = width - x;
const ratio = remainingWidth / (columns - i);
const column = smallColumns.includes(i + 1)
? ratio / MathUtils.mapLinear(n, -1, 1, 3, 4)
: ratio * MathUtils.mapLinear(n, -1, 1, 1.5, 2);
const adjustedColumn = i === columns - 1 ? remainingWidth : column;
for (let j = 0; j < rows; j++) {
temp.push({
x: x + adjustedColumn / 2 - width / 2,
y: j * row + row / 2 - height / 2,
scaleX: adjustedColumn,
scaleY: row,
});
}
x += column;
}
return temp;
}, [width, height, columns, rows]);
useFrame(() => {
for (let i = 0; i < squares.length; i++) {
const { x, y, scaleX, scaleY } = squares[i];
dummy.position.set(x, y, 0);
dummy.scale.set(scaleX, scaleY, 1);
dummy.updateMatrix();
mesh.current.setMatrixAt(i, dummy.matrix);
}
mesh.current.instanceMatrix.needsUpdate = true;
});
...Furthermore, remember that our instanceMesh count should be columns * rows:
<instancedMesh ref={mesh} args={[null, null, columns * rows]}>After all this, we will finally see a rhythm of a more random nature. Congratulations, you broke the grid:
Adding Color
Apart from using scale to break our grid, we can also use another indispensable element of our world; color. To do so, we will create a palette in our grid and pass our colors to our instances. But first, we will need to extract the palette from the picture. I just used a manual approach; importing the image into Figma and using the eyedropper tool, but you can probably use a palette extractor tool:

Once we have our palette, we can convert it to a list and pass it as a Component prop, this will become handy in case we want to pass a different palette from outside the component. From here we will use a useMemo again to store our colors:
//...
import { Color, MathUtils, Object3D } from "three";
//...
const palette =["#B04E26","#007443","#263E66","#CABCA2","#C3C3B7","#8EA39C","#E5C03C","#66857F","#3A5D57",]
const c = new Color();
const LygiaGrid = ({ width = 50, height = 86, columns = 12, rows = 10, palette = palette }) => {
//...
const colors = useMemo(() => {
const temp = [];
for (let i = 0; i < columns; i++) {
for (let j = 0; j < rows; j++) {
const rand = noise(i, j) * 1.5;
const colorIndex = Math.floor(
MathUtils.mapLinear(rand, -1, 1, 0, palette.length - 1)
);
const color = c.set(palette[colorIndex]).toArray();
temp.push(color);
}
}
return new Float32Array(temp.flat());
}, [columns, rows, palette]);
})
//...
return (
<instancedMesh ref={mesh} args={[null, null, columns * rows]}>
<planeGeometry>
<instancedBufferAttribute
attach="attributes-color"
args={[colors, 3]}
/>
</planeGeometry>
<meshBasicMaterial vertexColors toneMapped={false} />
</instancedMesh>
);As we did before, let’s explain point by point what is happening here:
- Notice that we declared a
cconstant that equals a three.jsColor. This will have the same use as thedummy, but instead of storing a matrix, we will store a color. - We are using a
colorsconstant to store our randomized colors. - We are looping again through our
columnsandrows, so the length of our colors, will be equal to the length of our instances. - Inside the two dimension loop, we are creating a random variable called
randwhere we are using again ournoisefunction. Here, we are using ouriandjvariables from the loop. We are doing this so we will get a smoother result when selecting our colors. If we multiply it by1.5it will give us more variety, and that’s what we want. - The
colorIndexrepresents the variable that will store an index that will go from0to ourpalette.length. To do so, we map ourrandvalues again from1and1to0andpalette.lengthwhich in this case is9. - We are flooring (rounding down) the value, so we only get integer values.
- Use the
cconstant tosetthe current color. We do it by usingpalette[colorIndex]. From here, we use the three.js Color methodtoArray(), which will convert the hex color to an[r,g,b]array. - Right after, we push the color to our
temparray. - When both loops have finished we return a
Float32Arraycontaining ourtemparray flattened, so we will get all the colors as[r,g,b,r,g,b,r,g,b,r,g,b...] - Now, we can use our color array. As you can see, it is being used inside the
<planeGeometry>as an<instancedBufferAttribute />. The instanced buffer has twoprops, theattach="attributes-color"andargs={[colors, 3]}. Theattach="attributes-color"is communicating to the three.js internal shader system and will be used for each of our instances. Theargs={[colors, 3]}is the value of this attribute, that’s why we are passing ourcolorsarray and a3, which indicates it is an array ofr,g,bcolors. - Finally, in order to activate this attribute in our fragment shaders we need to set
vertexColorsto true in our<meshBasicMaterial />.
Once we have done all this, we obtain the following result:

We are very close to our end result, but, if we check the original artwork, we see that red is not used in wider columns, the opposite happens to yellow, also, some colors are more common in wider columns than smaller columns. There are many ways to solve that, but one quick way to solve it is to have two map functions; one for small columns and one for wider columns. It will look something like this:
const colors = useMemo(() => {
const temp = [];
for (let i = 0; i < columns; i++) {
for (let j = 0; j < rows; j++) {
const rand = noise(i, j) * 1.5;
const range = smallColumns.includes(i + 1)
? [0, 4] // 1
: [1, palette.length - 1]; // 1
const colorIndex = Math.floor(
MathUtils.mapLinear(rand, -1.5, 1.5, ...range)
);
const color = c.set(palette[colorIndex]).toArray();
temp.push(color);
}
}
return new Float32Array(temp.flat());
}, [columns, rows, palette]);This is what is happening:
- If the current column is in
smallColumns, then, the range that I want to use from my palette is0to4. And if not, I want from1(no red) to thepalette.length - 1. - Then, in the map function, we pass this new array and spread it so we obtain
0, 4, or1, palette.length - 1, depending on the logic that we choose.
One thing to have in mind is that this is using fixed values from the palette. If you want to be more selective, you could create a list with key and value pairs. This is the result that we obtained after applying the double map function:

Now, you can iterate using different numbers in the makeNoise2D function. For example, makeNoise2D(10), will give you the above result. Play with different values to see what you get!
Adding a GUI
One of the best ways to experiment with a generative system is by adding a Graphical User Interface (GUI). In this section, we’ll explore how to implement.
First, we will need to install an amazing library that simplifies immensely the process; leva.
npm i levaOnce we install it, we can use it like this:
import { Canvas } from "@react-three/fiber";
import { Lygia } from "./components/Lygia";
import { useControls } from "leva";
function App() {
const { width, height } = useControls({
width: { value: 50, min: 1, max: 224, step: 1 },
height: { value: 80, min: 1, max: 224, step: 1 },
});
return (
<Canvas camera={{ position: [0, 0, 65] }}>
<Lygia width={width} height={height} />
</Canvas>
);
}
export default App;- We import the
useControlshook fromleva. - We use our hook inside the app and define the width and height values.
- Finally, we pass our width and height to the props of our Lygia component.
On the top right of your screen, you will see a new panel where you can tweak our values using a slider, as soon as you change those, you will see the grid changing its width and/or its height.
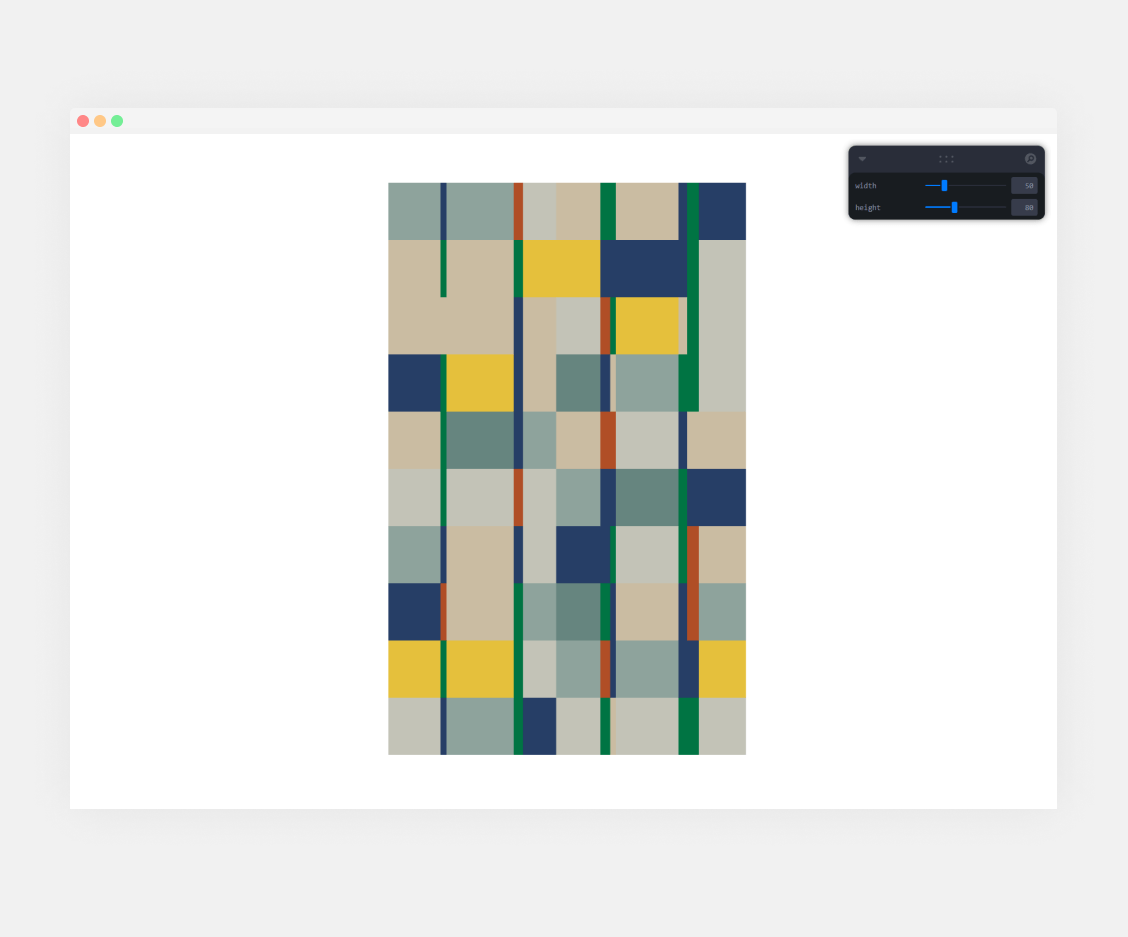
Now that we know how it works, we can start adding the rest of the values like so:
import { Canvas } from "@react-three/fiber";
import { Lygia } from "./components/Lygia";
import { useControls } from "leva";
function App() {
const { width, height, columns, rows, color1, color2, color3, color4, color5, color6, color7, color8, color9 } = useControls({
width: { value: 50, min: 1, max: 224, step: 1 },
height: { value: 80, min: 1, max: 224, step: 1 },
columns: { value: 12, min: 1, max: 500, step: 1 },
rows: { value: 10, min: 1, max: 500, step: 1 },
palette: folder({
color1: "#B04E26",
color2: "#007443",
color3: "#263E66",
color4: "#CABCA2",
color5: "#C3C3B7",
color6: "#8EA39C",
color7: "#E5C03C",
color8: "#66857F",
color9: "#3A5D57",
}),
});
return (
<Canvas camera={{ position: [0, 0, 65] }}>
<Lygia
width={width}
height={height}
columns={columns}
rows={rows}
palette={[color1, color2, color3, color4, color5, color6, color7, color8, color9]}
/>
</Canvas>
);
}
export default App;This looks like a lot, but as everything we did before, it is different. We declare our rows and columns the same way we did for width and height. The colors are the same hex values as our palette, we are just grouping them using the folder function from leva. Once deconstructed, we can use them as variables for our Lygia props. Notice how in the palette prop, we are using an array of all the colors, the same way the palette is defined inside the component,
Now, you will see something like the next picture:
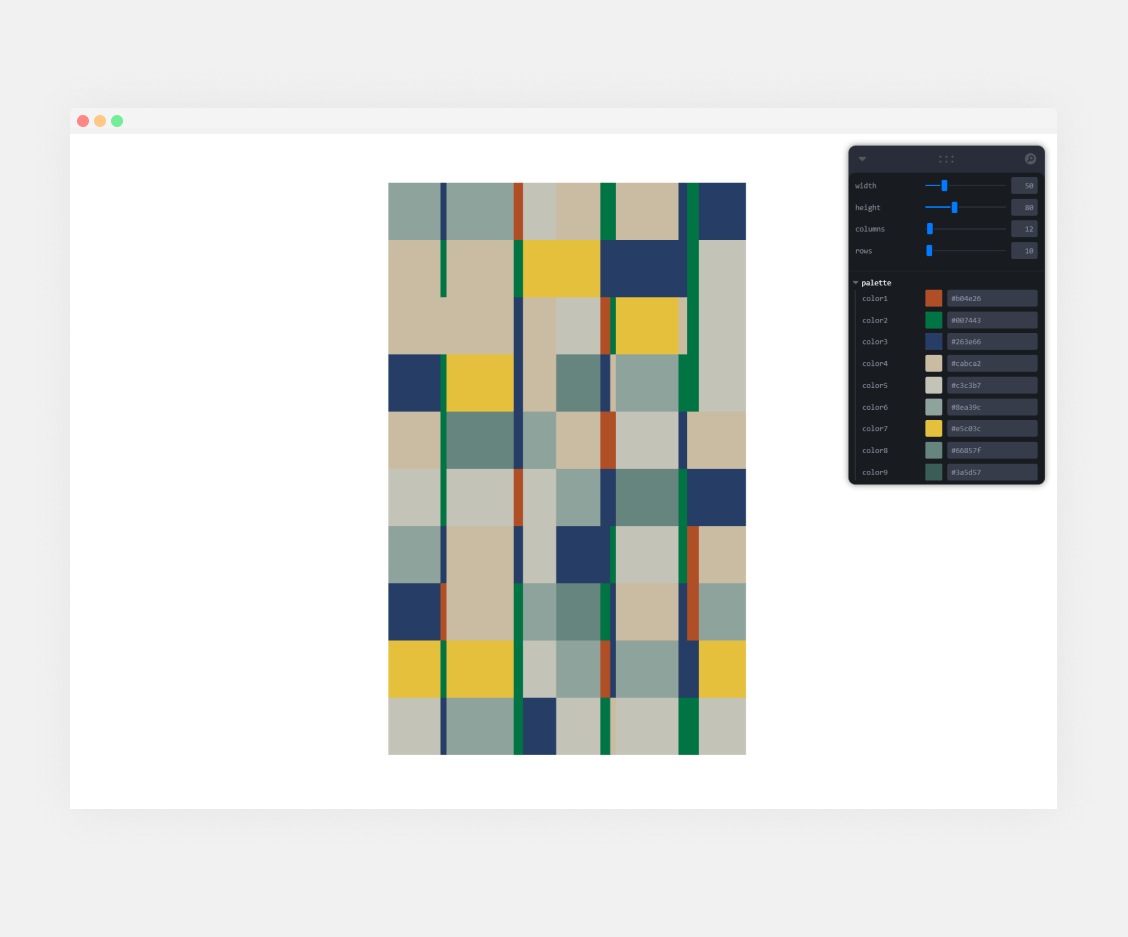
Awesome! We can now modify our colors and our number of columns and rows, but very quickly we can see a problem; suddenly, our columns do not have the same rhythm as before. That is happening because our small columns are not dynamic. We can easily solve this problem by using a memo where our columns get recalculated when the number of columns changes:
const smallColumns = useMemo(() => {
const baseColumns = [2, 4, 7, 8, 10, 11];
if (columns <= 12) {
return baseColumns;
}
const additionalColumns = Array.from(
{ length: Math.floor((columns - 12) / 2) },
() => Math.floor(Math.random() * (columns - 12)) + 13
);
return [...new Set([...baseColumns, ...additionalColumns])].sort(
(a, b) => a - b
);
}, [columns]);Now, our generative system is ready and complete to be used.
Where to go from here
The beauty of a grid system is all the possibilities that it offers. Despite its simplicity, it is a powerful tool that combined with a curious mind will take us to infinity. As a practice, I recommend playing with it, finding examples and recreating them, or creating something of your own. I will share some examples and hopefully, you can also get some inspiration from it as I did:
Gerhard Richter
If for example, I create a boolean that takes out the randomness of the columns and changes the color palette I can get closer to some of Gerard Richter’s abstract works:


Entering the third dimension
We could use color to represent depth. Blue represents distance, yellow indicates proximity, and red marks the starting position. Artists from the De Stijl art movement also explored this technique.

Other elements
What about incorporating circles, triangles, or lines? Perhaps textures? The possibilities are endless—you can experiment with various art, design, science, or mathematics elements.

Conclusions
In this article, we have had the exciting opportunity to recreate Lygia Clark’s artwork and explore the endless possibilities of a grid system. We also took a closer look at what a grid system is and how you can break it to make it uniquely yours. Plus, we shared some inspiring examples of artworks that can be recreated using a grid system.
Now, it’s your turn! Get creative, dive in, and try creating an artwork that speaks to you. Modify the grid system to fit your style, make it personal, and share your voice with the world! And if you do, please, share it with me on X.